As explained in the Toral Automorphism section, we can simulate dynamics on a torus by looking at flows on the space \(H=\mathbb{R}^2 / \mathbb{Z}^2\). In this space, we identify points that are integer translates. This means that every point in \(\mathbb{R}^2\) has a unique point in the 1-1 square \(H=\{(x,y) \ | \ 0 \leq x,y < 1\}\) that it identifies with, or in other words, \(H\) is a fundamental domain of \(\mathbb{R}^2 / \mathbb{Z}^2\).

When you mod \(\mathbb{R}^2\) out by \(\mathbb{Z}^2\), you identify \((x,0)=(x,1)\) and \((0,y)=(1,y)\). Thus, we can take our square \(H\) and imagine connecting the top and bottom to get a hollow cylinder. Then, we can take the left and right sides and connect them to get a donut looking object called a torus. Below is an animation of a simulated flow on a torus.

Note that even though there are visual discontinuities when the flow is visualized on the fundamental domain, they disappear whenever the flow is visualized on the torus, a representation that more accurately reflects the continuity of \(\mathbb{R}^2 / \mathbb{Z}^2\). This is because the fundamental domain \(\mathbb{R}^2 / \mathbb{Z}^2\) is well-defined and the cosets \(g + \mathbb{Z}^2\) (\(g \in \mathbb{R}^2\)) evenly tile \(\mathbb{R}^2\).

If we want to move to simulating dynamics on \(n\)-holed torus’, we have to look at dynamics on \(4n\)-sided polygons with sides identified in a similar way to the \(1\)-holed torus. Below is a diagram showing the sides identified on the octagon and the resulting \(2\)-holed torus construction courtesy of Cindy Grimm and John Hughes from Washington University.

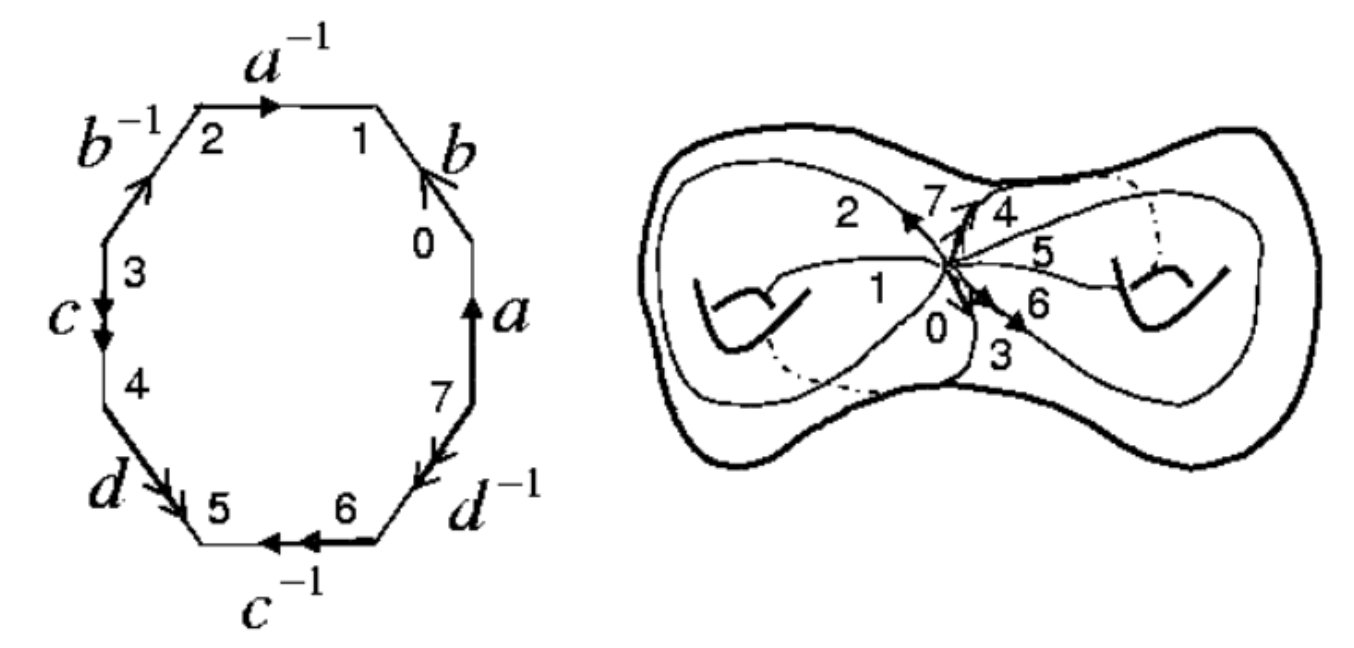
However, if we want to use a \(4n\)-sided fundamental domain to simulate the dynamics on a \(n\)-holed torus, the fundamental domain must be well-defined and the cosets must tile the space. We know from the Crystallographic Restriction Theorem that it is not possible to tile the Euclidean plane with an \(4n\)-gon fundamental domain. Thus, we must move to Hyperbolic Geometry.

In the hyperbolic geometry, we can construct a tiling of the hyperbolic plane by \(4n\)-gons. In the below animations, you will see a flow transversing a hyperbolic domain in the hyperbolic plane. The sides of the fundamental domain and the movement of the flow appear to be visually curved to our Euclidean eyes but are actually straight lines in the space. You will also see a record that keeps track of which sides the flow crosses above similar to the partioning of a cross-section shown in the Toral Automorphism section. As long as a flow does not traverse one of the corners (where the circle intersect) of the hyperbolic domain (a \(0\) measure subset of the possible flows), the coding above unqiuely determines a particular flow in the fundamental domain in what is called a Markov Coding.