As mentioned in the section on hyperbolic \(4g\)-gons, any genus \(g\) surface can be identified with a \(4g\)-gon in hyperbolic space by gluing the sides together in a particular way. Thus, once we have the flow within a given \(4g\)-gon in the hyperbolic disk, we can map that flow onto the corresponding surface. For \(g=1\), this is the map of the square to the 1-holed torus, which is easily given explicitly by the map

\[\phi_1: \mathbb{R}^2/\mathbb{Z}^2 \rightarrow \mathbb{R}^3\] \[\phi_1(x,y) = ((2+cos(2\pi y))cos(2\pi x),(2+cos(2\pi y))sin(2\pi x),sin(2\pi y))\]

However for genus \(g>1\), such a map is much harder to give explicitly.

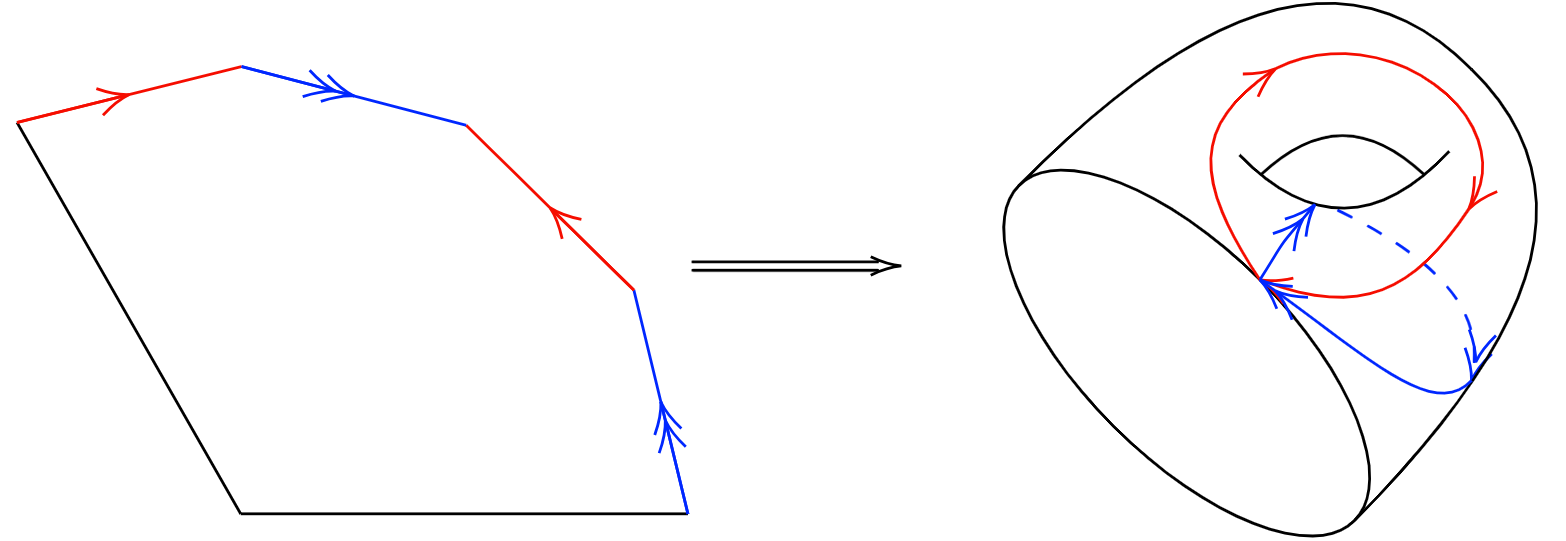
Conceptually, the way in which a \(4g\)-gon maps into a genus 4 surface is well understood, as demonstrated by the image in the section on hyperbolic \(4g\)-gons that maps an octagon to a 2-holed torus. By numbering the sides of an octagon 1 through 8, the mapping is given by identifying the following pairs of sides (1,3), (2,4), (5,7) and (6,8).

For larger \(g\), we can continue this pattern, taking each group of 4 sides, and identifying side 1 with 3 and aide 2 with 4 within that group. As it turns out, each of these 4-sided sections of a \(4g\)-gon map to a genus 1 section of a genus \(g\) surface, topologically equivalent to a punctured torus, in the same way. This allows us to generalize these higher \(g\) mappings by only looking at the map from a single \(4g\)-sided section into a single copy of the punctured torus with the puncture stretched out to allow for easy stitching together of the different pieces, as seen below.

The explicit map from this sector to the corresponding punctured torus depends on your choice of imbedding of the torus into \(\mathbb{R}^3\). Because we are trying to show the hyperbolic flow, it is more favorable for our visualizations if the imbedding we chose is as simple as possible. Because of this, we imbed the \(g\)-holed torus as a \(4g\)-gon prism with rounded edges and holes near each lateral edge, see below. Explicitly, these are drawn as a set of piecewise functions, which means our map for the 4-sided sector of our \(4g\)-gon must also be a set of functions that map into each region. An image of the corresponding regions in the hyperbolic polygon and the punctured torus is shown below for the \(g=2\) case.

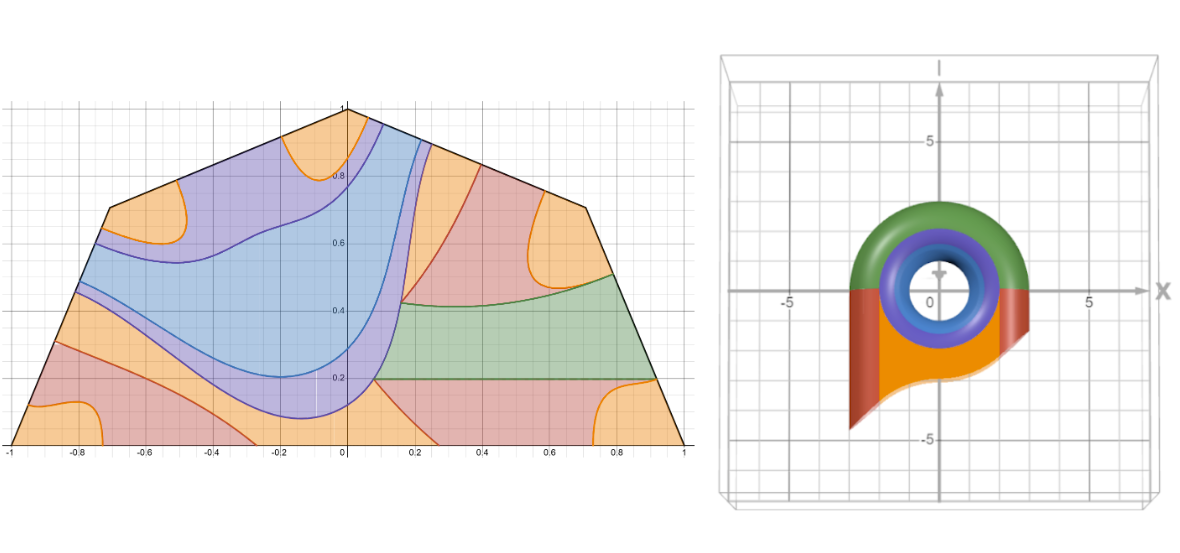
{Image of regions in an octagon to a punctured torus}

It is impossible to map the \(4g\)-gon to the \(g\)-torus without some apparent stretching. Here the term apparent refers to the fact that our maps need to go from the unit disk, which is flat, to the \(g\)-holed torus, which is hyperbolic. We map from the unit disk because of our choice to represent these \(4g\)-gons in the poin-care disk. The hyperbolic-ness of our visualizations in the disk come from our non-constant distance metric. Therefore, to preserve this hyperbolic-ness as much as possible, our maps need to minimize the Euclidean distortion between the disk and \(g\)-torus as much as possible. Furthermore, we need to make sure that the level of stretching of our different maps, corresponding to the different regions of the 4-sector, agree with each other on their shared boundaries, and for our resulting geodesic visualization to appear smooth, we need that the derivatives of the maps agree as well.

Once we have our maps, we can take our geodesics from the poin-care disk, and see how they flow on a hyperbolic surface.