Introduction

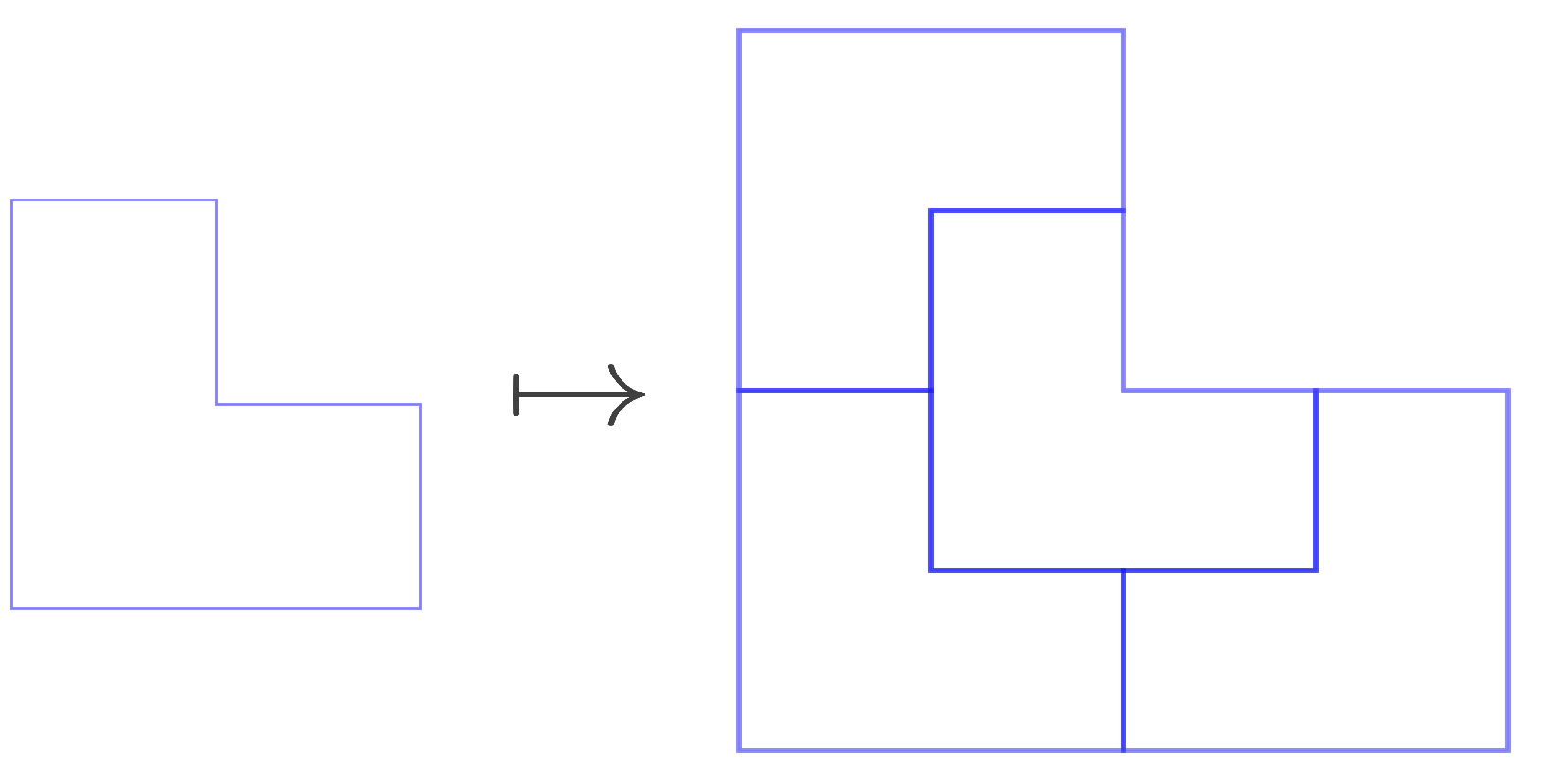
Given a set of (well-behaved) polygons, there are many ways to arrange them to fully cover the real plane, such that the pattern is everywhere non-repeating, or aperiodic. A particular such pattern is called an aperiodic tiling. Many such aperiodic tilings arise from a substitution rule - a way to arrange the given polygons to form a scaled-up version of those same polygons (see below for an example using the Chair Tiling). In the limit, this gives infinitely many ways to cover the entire plane without repetition. The many different possible tilings of \(\mathbb{R}^2\) which arise from a substitution rule lead to a topological space called a tiling space, the study of which has been of particular interest to mathematicians and materials physicists since the 1970’s.

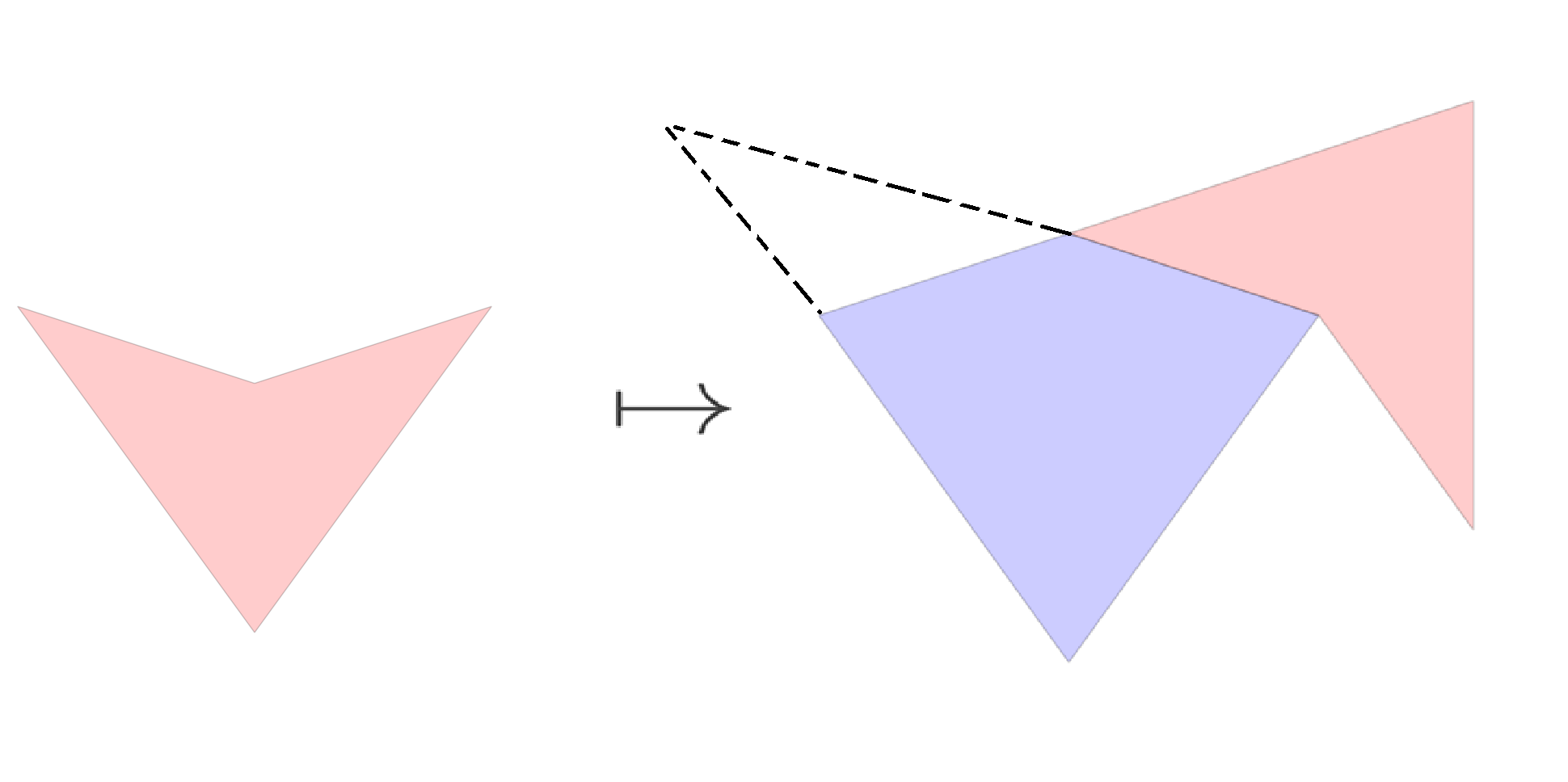
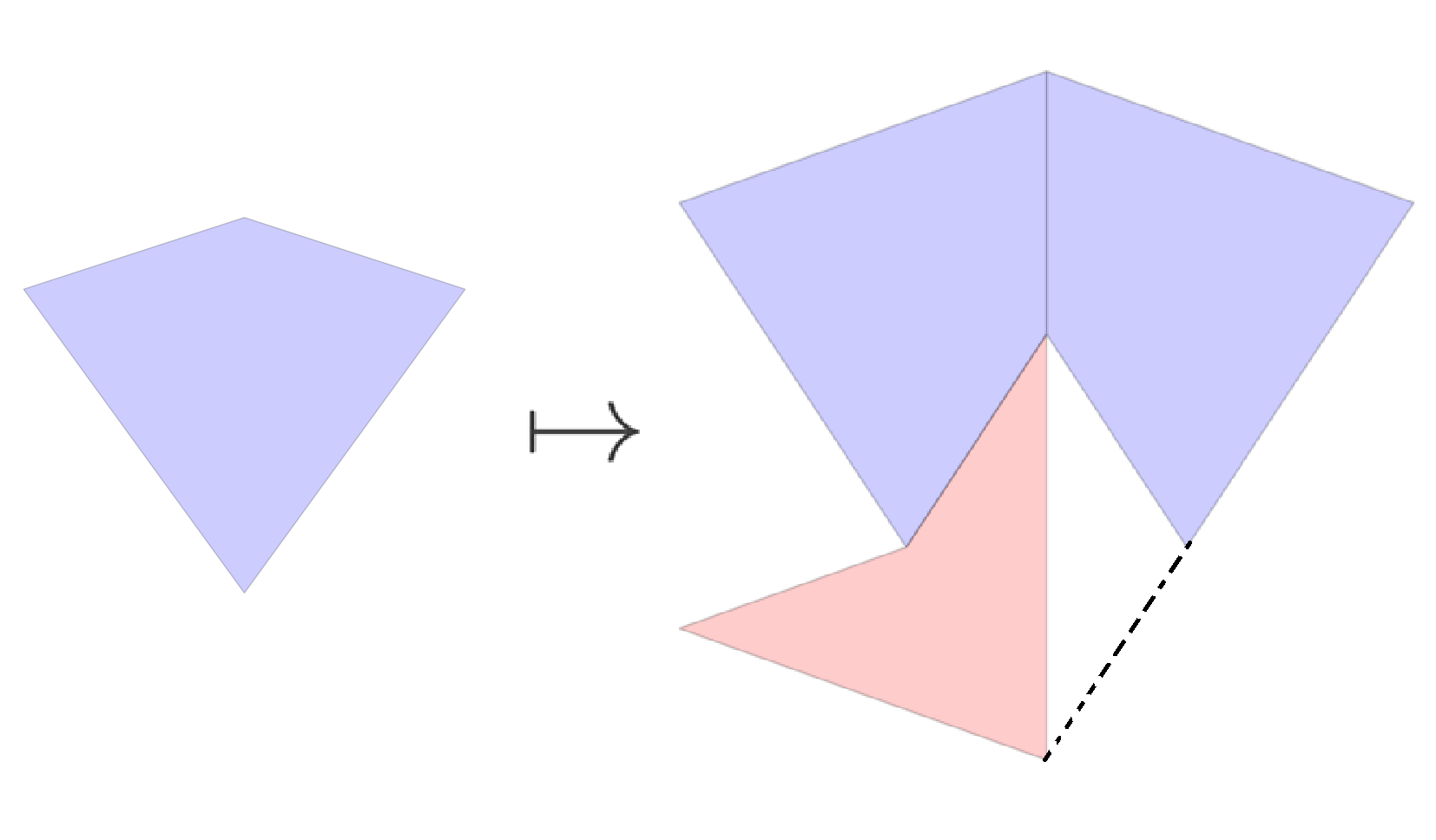
Along with traditional substitution rules, some aperiodic tilings can arise from ‘pseudosubstitution rules’, also called substitution-with-amalgamation. In these cases, rather than forming a scaled-up version of the initial shapes, the substitution creates a new shape which may have missing corners, or parts jutting outside of the original. See below for an example, using the Penrose Kite-Dart pseudosubstitution.

Explicitly computing topological invariants on arbitrary aperiodic tilings is difficult, but can be made easier by rewriting the substitution rule into one which behaves more nicely. In particular, for a standard substitution, we can ‘collar’ - decorate the tiles with descriptions of their neighbors - to obtain such a substitution. Pseudosubtitutions do not have quite the same structure as regular substitutions, yet we would like to be able to analyze them in a similar way. In particular, when working with pseudosubstitutions, we can rewrite the substitution rule in the same way, but doing so would require collaring possibly more than once (i.e. decorating with not only direct neighbors, but also neighbors-of-neighbors, etc.).

Our goal for this project is to develop a script which can take in arbitrary pseudosubstitutions and find the rewritten substitution rule in order to directly compute certain topological invariants.

Future Work

Our goal is to finish constructing the AP-complex for the chair tiling and the Penrose kite dart tiling (see under Mathematical Background for more information). This means writing the induced substitution rule on \(k\)-collared prototiles and determining all possible identifications of boundaries of \(k\)-collared prototiles. For the Penrose kite dart, we need to write code to determine the \(k\) such that the \(k\)-collars form the AP-complex. Additionally, we need to write code to determine when we have found all possible \(k\)-collars (i.e., when can we stop searching supertiles for \(k\)-collars).

All our code should be able to be generalized for any pseudosubstitution tilings. The next tiling we would like to work on is the Godreche-Lancon-Billard binary tiling. Ultimately, the goal is to explicitly compute topological invariants from the resulting branched manifold and corresponding induced self-map, i.e. cohomology groups.

Progress

Our current progress can be found on GitHub.

Chair Tiling:

• We have coded the substitution rule; as in, we can generate and display any n-level supertile

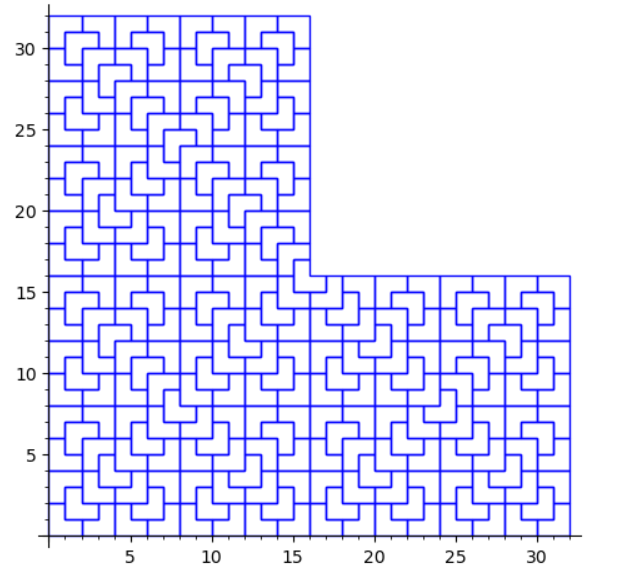
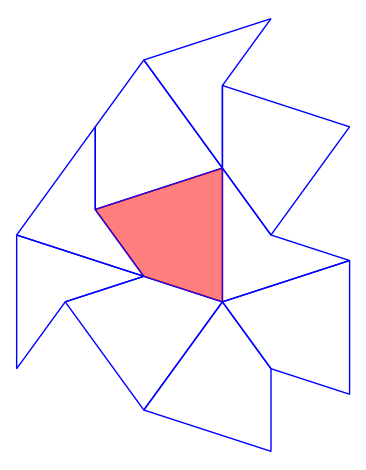
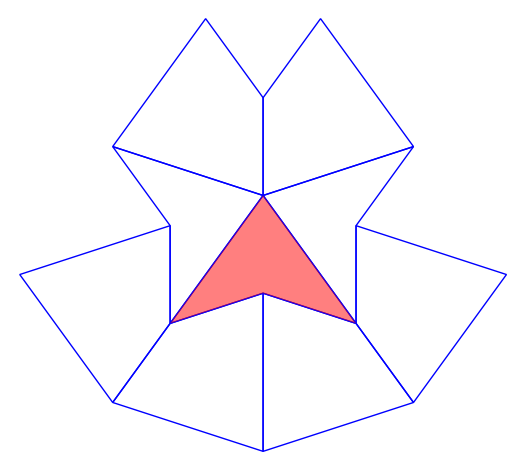
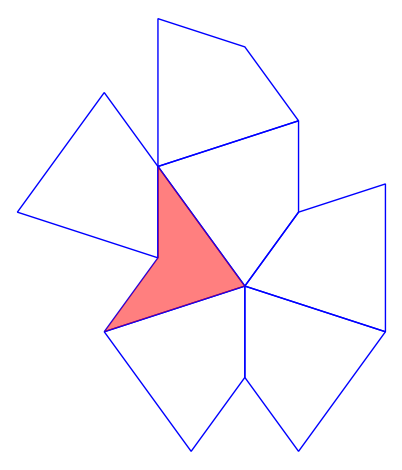
• Wrote code to find all k-collars for a given k. We ran the code to find all 56 1-collars, here are some examples!:

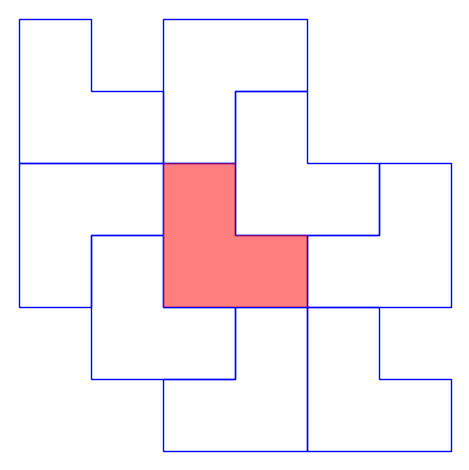
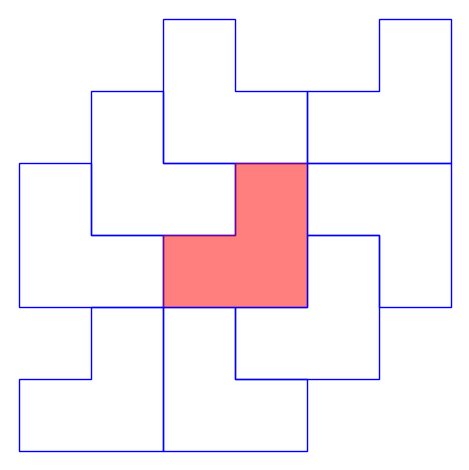
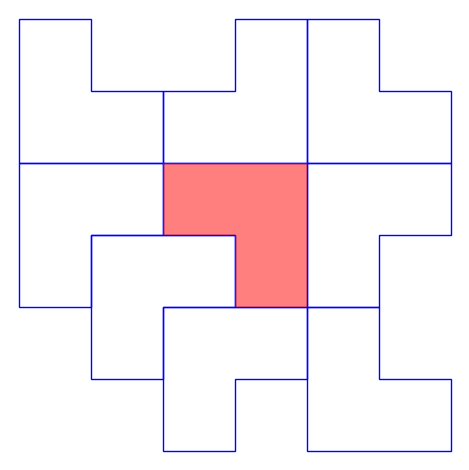
Penrose Kite and Dart Tiling:

• We have coded the substitution rule

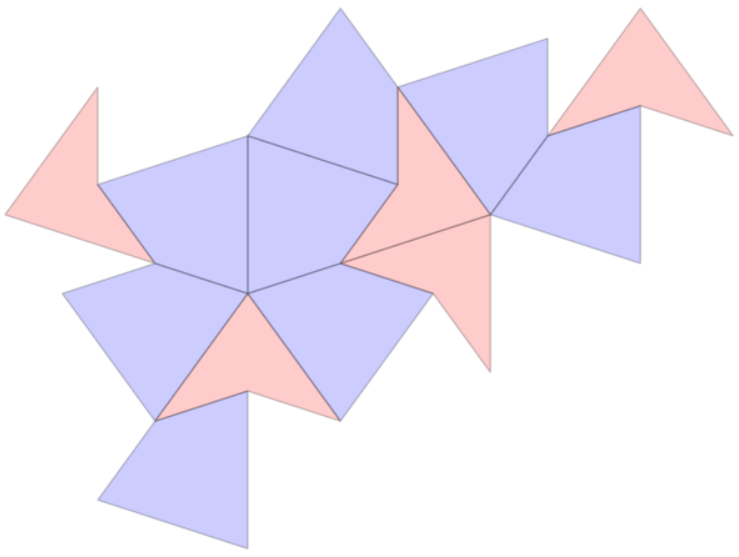
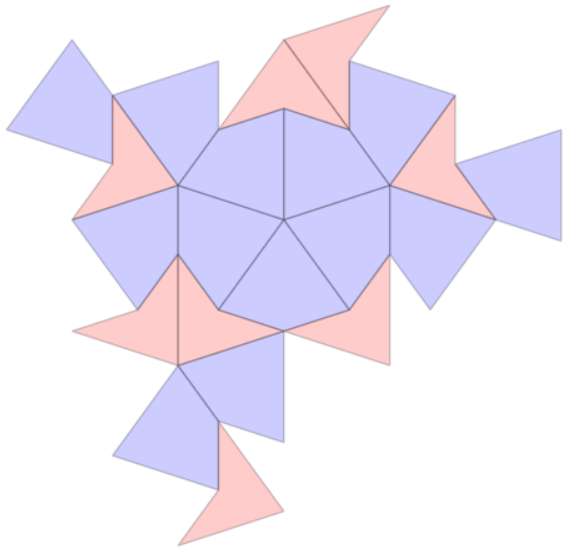
• We have looked through the level 3 kite and dart supertiles for 1-collars, but we have not yet found all possible 1-collars. We also need to filter out any incomplete collars we find

Some Next Tasks:

• Complete code to find all k-collars of Penrose tiling
• Make substitution rule more efficient by implementing it with a python dictionary

Our code can be easily generalized to work with other substitutions, once the substitution rule is written. We hope to make the program more accessible to other researchers once we have expanded its functionality.

Mathematical Background

There are two ways to consider a tiling space. One is identifying it with the standard Euclidean space \(\mathbb{R}^2\) and define what the open sets are. The other way is to identify it using inverse limit. Let me first introduce the purely topological definition.

Definition (Open sets in tiling spaces) A basic open set \(C(P,U)\) of a tiling space are defined by two parameters: a patch \(P\) and a set \(U\) denoting all the possible locations of the origin relative to that patch.

We define the intersection rule as follows: for two open sets \(C(P,U)\) and \(C(Q,V)\), the intersection is defined as \[ C(P,U) \cap C(Q,V) = C(P \cup Q, U \cap V) \] In other words, we consider a larger patch, yet restricting the choice of origins relative to the patch. We can also define tiling spaces as inverse limits. First,

Definition (Inverse limit space) Let \(\Gamma_0,\Gamma_1,\ldots\) be topological spaces, and for each non-negative ingeter \(n\), \(f_n \colon \Gamma_{n+1} \to \Gamma_n\) is a continuous map. Consider the product space \(\prod \Gamma_i\) equipped with the product topology. Then the set \[ \varprojlim(\Gamma,f) = \left\{ (x_0,x_1,\ldots) \in \prod \Gamma_n \mid x_n = f_n(x_{n+1}) \right\}\] is called the inverse limit space.

Works from many people have been done to construct tiling spaces from inverse limits. As our goal is to compute topological invariants, we are most interested in the Anderson-Putnam (AP) construction.

Anderson-Putnam (AP) Construction

Let \(\sigma\) be a substitution with linear stretching factor \(\lambda\). Let \(\Gamma_0\) be the set of all possible instructions for laying a tile at the origin, with one copy of each tile type, stitched together at edges. Define \(\Gamma_n\) to be \(\Gamma_0\) expanded by a factor of \(\lambda^n\). Then \(\Gamma_n\) contains one copy of each supertile of level \(n\). \(\Gamma_0\) tells us how to place a tile at the origin, and \(\Gamma_n\) tells us how to place a supertile of level \(n\) that contains the origin. The maps \(f_n \colon \Gamma_{n+1} \to \Gamma_n\) are forgetful maps that restricts attention to the level-\(n\) supertile containing the origin.

Definition (Forcing the border) A substitution is said to force the border if there exists a positive integer \(n\) such that any two level-\(n\) supertiles of the same type have the same pattern of neighboring tiles.

In this case, a level-\((n+k)\) supertile determines all of the level-\(k\) supertiles around it, and an infinite supertile determines the entire plane. Points in the inverse limit \(\varprojlim(\Gamma,f)\) are then in 1-1 correspondence with tilings of the plane, and we have a topological isomorphism between the inverse limit space and the topological space. It implicitly tells us that if a substitution rule forces the border, then it expands to the entirety of \(\mathbb{R}^2\). There are substitutions where not all \(\mathbb{R}^2\) is filled after infinite repetition, i.e. not all substitution rules force the border.

One clearly could see that, in this example, if we keep substituting it would only fill out the first quadrant. To resolve this issue, Anderson and Putnam proved that for substitutions, if we start with tiles that are collared once and rewrite the substitution rule, then this new substitution rule expressed using 1-collared tiles indeed forces the border. As we are also interested in pseudo-substitutions, collaring once may not be enough in general to obtain a substitution rule that forces the border. As part of the project, we are working on a systematic way to produce the level of collaring needed to produce such substitution rules, given the original substitution rule.